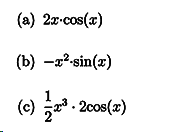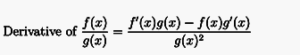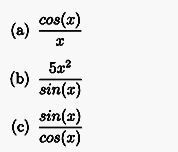If you studied part 1 of this course, you would be familiar with differentiating polynomials and trigonometric functions. You would also be aware of how important differentiation is for exam 1! (Approximately 25%!) Now for two fundamental rules: the Product Rule and the Quotient Rule.
Product Rule
Unlike for addition and subtraction where you can differentiate one term at a time, differentiating the product of two expressions is more complicated. Suppose you want to differentiate the function :
5x sin(x). You would be forgiven for thinking the answer is 5 cos(x). However, it is not! Since we have a product (multiplication), you need to apply the following rule :
( f(x)g(x) )’ = f’(x)g(x) + f(x)g’(x)
Although that might look complicated, it really isn’t. If you have a multiplication, do the derivative of the first times the second + the first times the derivative of the second.
The derivative of 5x is 5. The derivative of sin(x) is cos(x) (you should know that from part 1 of this course). So the derivative of 5x sin(x) is :
5 sin(x) + 5x cos(x)
Take the time to scrutinize that example until you understand it. Once you’ve got the hang of it, try the following exercise.
Exercise
Find the derivative of the following functions :
Quotient Rule
The Quotient Rule is similar to the Product Rule in the sense that you can’t just do the derivative of the numerator divided by the derivative of the denominator. Once again, there is a formula :
For example :
Once again, scrutinize every detail. It might take time, but the first step to mastering the technique is understanding how it is applied. Once you understand the example practice, practice, practice!
Exercise
Find the derivative of the following functions:
About Learnmate
Learnmate is a trusted Australian community platform that connects students who want 1:1 or small group study support, with tutors who are looking to share their knowledge and earn an income. From primary school to high school subjects — from science and maths to niche subjects like visual communication — Learnmate can help you improve academic performance or boost confidence, at your pace with the tutor that you choose.
We pride ourselves in offering a reliable and positive experience for both our students and tutors. Every tutor that joins the platform is vetted to meet a level of academic excellence, teaching qualification or relevant experience. All tutors are provided the opportunity to complete professional training.
Students and parents can easily find and screen for tutors based on their location, their subject results or skill level, and whether they provide in-person or online sessions. Learnmate is proud to provide tutors in Melbourne, Sydney, Geelong, Brisbane, Hobart, Canberra, Perth & Adelaide, and other locations.