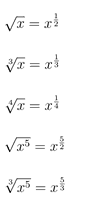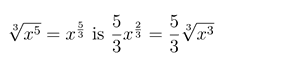Once you know basic differentiation and can use both the Product and Quotient Rules, you need to get the hang of differentiating more tricky expressions. This short course will help you do just that with tips and tricks, not to mention a few exercises to get the hang of it too! If you want to benefit from this, be sure to spend a good hour at making sure you understand every step in the worked examples. If it’s too tricky, ask a tutor or someone who knows!
Exponential
An exponential expression is when you elevate a number to the power of x, for example :
2x ax ex and so on…
The derivatives are EASY, it’s just the same expression multiplied by loge of the number under the power. So for our 3 expressions in the preceding paragraph, the derivatives are :
2x loge(2) ax loge(a) ex loge(e) = ex
The last case is a special one because loge(e) = 1. You need to remember the very special case that the derivative of ex is ex ! It doesn’t change!
Tip: if a number is multiplying the exponential, it doesn’t influence the derivative. For example :
- The derivative of 5ex is also 5ex.
- The derivative of 3 . 2x is 3 . 2x loge(2)
Logarithms
The derivative of a log with any base “a” of x is: 1 / (x . loge(a))
In the special case where the base is “e” the derivative is simply 1 / x
Notation : Sometimes loge(x) is written ln(x) (pronounced “natural log of x”)
Roots
The derivative of roots can be found the same way as the derivative of polynomials. You simply need to transform the root into an appropriate power of x. For example :
So using the usual method of differentiation for polynomials, bring the power to the front, then bring the power down by one unit. For example :
The derivative of
Exercises: Find the derivatives of the following expressions.
About Learnmate
Learnmate is a trusted Australian community platform that connects students who want 1:1 or small group study support, with tutors who are looking to share their knowledge and earn an income. From primary school to high school subjects — from science and maths to niche subjects like visual communication — Learnmate can help you improve academic performance or boost confidence, at your pace with the tutor that you choose.
We pride ourselves in offering a reliable and positive experience for both our students and tutors. Every tutor that joins the platform is vetted to meet a level of academic excellence, teaching qualification or relevant experience. All tutors are provided the opportunity to complete professional training.
Students and parents can easily find and screen for tutors based on their location, their subject results or skill level, and whether they provide in-person or online sessions. Learnmate is proud to provide tutors in Melbourne, Sydney, Geelong, Brisbane, Hobart, Canberra, Perth & Adelaide, and other locations.