Hi there! My name is Daniela and I am a VCE Math Methods and Biology tutor on Learnmate. I graduated from John Monash Science School with an ATAR of 98.85 and scaled study scores of 49 for Math Methods and Biology, also achieving 45+ in Chemistry and Physics. I’ve been a passionate tutor for the past 3 years and I’m here to provide you insight into how to set yourself up for success in VCE!
Composite functions are a common struggle topic for students, but fear not – with the right guidance, you can navigate them successfully in VCE Maths Methods. This blog post serves as your compass, providing clarity on what composite functions are and how to approach them effectively.
Understanding Composite Functions: The Basics
Composite functions involve combining two functions to create a new one. Let's break it down: if you have two functions, f(x) and g(x), their composite, written as (f∘g)(x) or f(g(x)), means applying g first and then f. It's like a chain reaction where the output of one function (g(x)) becomes the input for the other (f(x)).
The condition that must be fulfilled for a composite function to exist is:
“The range of the inside function must be a subset of the domain of the outside function”
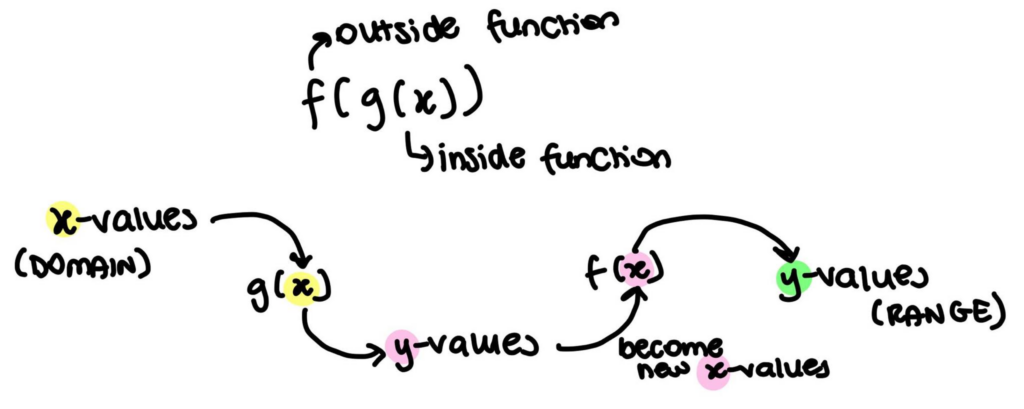
This condition exists because the inside function (e.g. g(x) for f(g(x))) outputs y-values (the range) which become the x-values (the domain) of the outside function (f(x)). Another way to think about it is that for (f∘g)(x), it essentially means applying function g to x first, then taking that result and applying function f.
Example
As shown in the example, f(g(x)) did not need any adjusting of ranges/domains since the range of the inside function was a subset of the domain of the outside function (in this case, it was exactly the same). For g(f(x)) however, the range of the inside function, f(x), included zero, whereas the domain of the outside function, g(x), did not. This can not work for a composite function because the output of f(x) including zero, can not go as an input into g(x). Therefore you restrict the domain of f(x), so that it’s range does not include zero. In case, the new domain would be R\{0}, therefore making the new range (0,∞). |
Domains and Ranges of the Composite Functions
A very common question in Maths Methods is to first find the composite function and then to state its domain and range. Simply put, the domain of the composite function is the domain of the inside function, because this is where you are putting your x-value into first. The range of the composite function is then based on this range that is outputted and then put into your outside function (generally drawing a quick sketch or mapping out a couple of values can give you a general idea to get the range). This question however becomes much more complicated and error-prone when you have had to restrict the domain of the original inside function (like shown in the example above). The main thing to keep in mind is that you are putting your x-values into the inside function. These y-values are inputted into your outside function which give you new y-values! This can all be a bit confusing but hopefully the diagram below can help!
How to Approach Composite Function Questions
There is a general method outlined below, however it is important that you remain vigilant and aware of what is being asked in the question.
- Write out the domain and ranges of both the inside and outside functions given: This will set you up well to complete the rest of the question. (Draw a quick graph of each if you like).
- Identify if the range of the inside function is a subset of the domain of the outside function:
- IF NOT: You need to adjust the domain of the inside function so that it’s range becomes a subset of the domain of the outside function.
- IF YES: No changes need to be made
- Write out the composite function rule with the correct notation.
- Identity that the domain of the composite function is equal to the domain of the inside function. Identify the subset range based on these outputted values as described previously.
- Finally, check that your domain and ranges make sense in the context of your final function! This is often just a quality to check to make sure that you haven’t accidentally missed something.
Common Mistakes Students Make
- Not restricting the domain appropriately: Students often forget the condition needed for a composite function or they forget that they had changed the domain/range of the inside function earlier. Ensure that you annotate your working so that it is very clear what has been changed throughout the question!
- Improper notation: Ensure that your notation for your composite function is appropriate and you are using the same assigned letters as given in the question. For example, if they used v(x) and d(x), you are writing your final answer using v and d! Furthermore, be careful with your domain and range notation, especially on whether you are including or excluding a value!
- Set-up your answer: Taking a few minutes to set-up your answer can make a huge difference in both understanding the question but also avoiding silly mistakes. Take the extra time to just write out the domains and ranges, setting yourself up for success.
Conclusion
Overall, composite functions can be tricky, but with practice and understanding, you will stand out among other students. Visualising the functions graphically and practicing regularly are keys to mastering composite functions. As you delve into this topic, remember that it's not just a mathematical concept but a valuable problem-solving tool with real-world, exciting applications. Happy exploring!
This blog is the third in a series dedicated to uncovering the essential skills and strategies necessary to succeed this year in VCE Maths Methods. See also the first and second blogs in this series for more insights! Stay tuned for future blogs as we continue to dive deeper into this subject, aiming to equip you with a comprehensive toolkit for success.
This blog was written by Daniela L, a VCE Biology and VCE Maths Methods Tutor on Learnmate. Daniela is tutoring while studying a Bachelor of Advanced Science Research at Monash University. She graduated with a 98.85 ATAR, 45+ study scores in 4 subjects and has been supporting other students achieve their goals through tutoring for over 3 years.
You can view her profile and, subject to her availability, request Daniela as your tutor here.