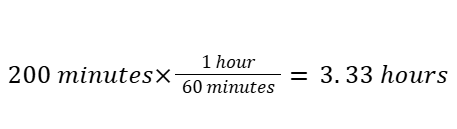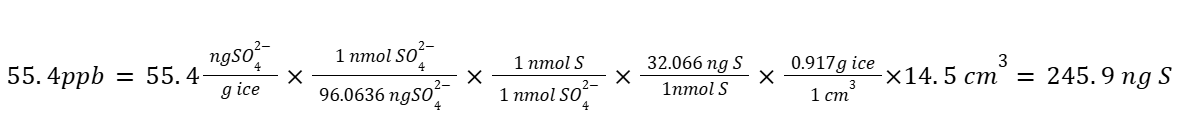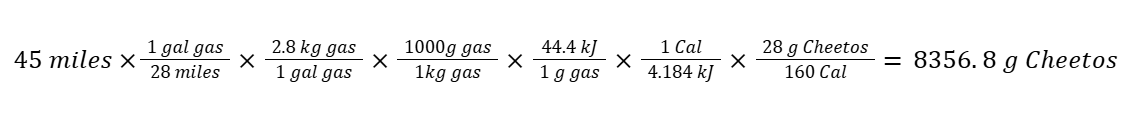“Gasoline has an energy content of 44.4 kJ/gram. How many grams of Cheetos are needed, at minimum, to equal the amount of energy required for a car to travel 45 miles assuming the car gets 28 miles/gallon? Note: One (1) gallon of gas weighs 2.8 kg and 28g of Cheetos has 160 food calories.”

While I don’t know all of the professors and instructors of chemistry, I feel confident in saying that missing units rank in their top 10 annoyances when marking homework or exams. It seems like every student has forgotten units at some point or another. Even those of us in the industry will forget units when hastily scribbling notes on a dilution or a formula to remember. In both cases, it isn’t the writer’s fault. They know what the unit is meant to be at that moment. But, a year from now, that missing unit has long since been forgotten.

I had this happen to me when I needed to confirm some measurements for a paper I was writing. I looked back at all of my well-organised notes and there, staring back at me, was a page full of math — but not a unit in sight. I couldn’t believe that I had become that chemist. I had preached “Don’t forget the units!” to countless students, and yet I had forgotten my units.

The Trouble with Missing Units in Chemistry

So, what is the trouble with units, and why are we so prone to forget them?

For younger students, some blame lies in not being forced to consistently write them in earlier science and math classes. When solving word problems, the unit is usually stated in the question, so it’s easy to just answer with a number.

“If Jane rode her bike 3km to the store, then 2km to her friend’s house, and then another 1km back home, how many kilometres did Jane ride her bike?”

Since the question clearly states kilometres, students simply add 3 + 2 + 1 and write “6.” The instructor often marks it correct without pushing for the unit.

But what happens when the unit isn’t specified? Imagine asking someone how far it is to the market. It's faster to ask, "How far is it to the market?" rather than, "How many kilometres do I need to travel to the market?" There’s often a shared understanding, but this breaks down without a common context — especially for outsiders or new learners.

In Chemistry word problems, context is usually given, but the unit might be implied or missing. For example:

• "How many millilitres (mL) of the acid are needed to neutralize the base?" (Specific volume asked)

• "How much acid is needed to neutralize the base?" (No specific unit stated)

If a student answers simply “12” without specifying the unit, the instructor is left guessing whether they meant millilitres, moles, or something else entirely. This confusion is why the importance of units in chemistry cannot be overstated.

Without written units, even a correct number can lose all meaning.

Dimensional Analysis: A Better Way to Understand Units

The real challenge (and fun) in chemistry comes when students are asked to find the amount of something needed without a preset formula — like how many grams of Cheetos to fuel a car.

Many students panic because they aren’t explicitly taught flexible unit conversion through ratio reasoning. They are taught specific formulas but not how to "follow the units."

This is where dimensional analysis shines. Instead of memorising formulas, dimensional analysis uses ratios to systematically cancel out units, guiding you directly to the answer.

For example, converting 200 minutes to hours:

Or converting 1.5km to metres:

Notice: by stacking units properly, you don't need to memorise whether to multiply or divide — the units tell you what to do.

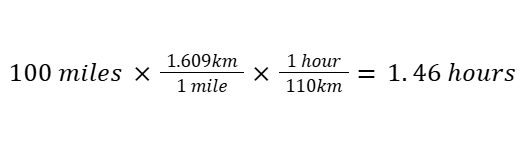
Here’s a more complex example: finding the driving time for 100 miles at an average speed of 110 km/hr.

Traditional method (less clear):

100×1.609=160.9

160.9÷110=1.46

Using dimensional analysis in chemistry (clearer, with units cancelling):

Every unit cancels systematically, and you know the final unit is hours — no confusion.

Putting It All Together: Why Units Matter

In chemistry, dimensional analysis proves extremely useful for complex multi-step problems. Imagine needing to convert 55.4 ppb SO₄²⁻ in 14.5 cm³ of ice (density 0.917 g/cm³) to nanograms of Sulfur:

By carefully managing the units, even the most intimidating problems become manageable.

And yes — using dimensional analysis, students could figure out that it takes approximately 8357g of Cheetos to fuel that car:

Conclusion

The importance of units in chemistry lies in their ability to give meaning to numbers. Without units, calculations are meaningless, and communication breaks down. By encouraging students to use dimensional analysis and to consciously include units in every answer, we can help them avoid mistakes, build better scientific habits, and succeed not just in exams — but in real-world chemistry practice.

If you found these helpful, I’d personally love to support you as your tutor this year. You can view my profile here on Learnmate and contact me to discuss tutoring.

Alternatively, you can also engage other tutors on Learnmate to help you refine your study strategies, boost your confidence, and receive personalised support for Chemistry. Connect with an expert Chemistry tutor on Learnmate and take your understanding to the next level!